Optical simulation room(9)
■ポロプリズム双眼鏡のケラレの話(前編)
プリズム双眼鏡で射出瞳の4辺がケラレている双眼鏡は光をロスっているからお勧めしない。 これは入門書によく出てくる話です。


ケラレのある射出瞳例(BK7プリズム) ケラレのない射出瞳例(BaK4プリズム)
しかし現実にはホームセンターの双眼鏡コーナー(安物)を探しても、ケラレの見本のようなモノにはなかなかお目にかかれません。
高倍率ズーム式がトレンドになっているため、射出瞳自体がとても小さくなっていて分かりにくいのです。
お店にケラレている写真を撮りに行ってみたのですが出来なかったので、安物双眼鏡とそうでない双眼鏡の射出瞳をシミュレーションしてみました。(上図)
安物はポロプリズムの硝材に安価なBK7プリズム(屈折率が低い)を使い、そうでないものは硝材にBaK4(屈折率が高い)を使っています。
たしかに安物は4辺が薄青くケラレていますが、良く見ると各辺でボケ方が違いますね。
そう、射出瞳は対物レンズの輪郭の円を見ているのですが、ケラレはそのかなり手前のプリズム反射面で起こります。
ボケの小さいほうのケラレは対物レンズに近い第一ポロプリズム、ボケの大きいほうのケラレは第二ポロプリズムによるものです。
第二ポロプリズムによるケラレはボケボケになるので分からないかもしれません。 正確には4辺のケラレのボケ方は全部異なります。
次にケラレのないほうの双眼鏡ですが、真後ろから射出瞳を見るのではなくて、見かけ視界の辺縁部の射出瞳を見たらどうなるでしょうか?

こんな感じで、機種によって程度は異なりますが、薄青いケラレが現れることがあります。
双眼鏡の角度を振ったまま 360°コマの軸が倒れるように回転させて観察してみてください。
回転角度によってケラレる所とそうでない所がありますね。
もし360°どこに回しても青いケラレが見えなかったらその双眼鏡はかなり優秀か、あるいは実視界がそんなに広くない機種です。
ところで、プリズムのケラレとは反対側に三日月状のケラレがあることに気がつきましたか。
それはプリズムによるケラレ(一定の角度にある)と違い、傾けていくほど徐々にケラレていくのが分かると思います。

これは対物レンズや接眼レンズでのケラレ(ビネッティングといいます)によるもので、プリズムのケラレとは別物です。
プリズム以外の部分のレンズの直径不足や鏡筒の内壁によって斜めの光線がケラレることなどによって起こり、機種によって程度は異なります。
広視界のわりに接眼レンズが小径にできている機種では接眼レンズの直径方向の余裕が小さいため接眼レンズでのビネッティングが大きくなる傾向があります。
先日、ビクセンのSW8X25WPの正立光学系がBaK4(プリズム)+ミラーの構成であることを取り上げました。
同社のアスコット SW10×50(実視界8.5°)や五藤テレスコープのStar Cruise425(実視界14.5°)も同様にミラーを併用した「ハイブリッド」正立光学系ですね。
ミラーをつかえばプリズム硝材の屈折率によるケラレの制約から逃れられます。 板を4枚組み合わせるだけなので低コストで軽量化できるかも。
ミラーを使うのが良いのならいっそ4面ともミラーにしてしまえば良いのに・・・とも思えるのですが、4面ともミラーだと組立てにくいのでしょうか。
それとも透過率が下がるから? アルミや高反射アルミでは4面も使ったら致命的に暗くなるから誘電体多層膜ミラーが要りますけどね。
ミラーとプリズムとを組み合わせる場合、接眼レンズ側をプリズムにすると射出瞳でのケラレ(あくまで見かけ上)、はボケて目立たなくできます。
まあそれでもケラレ自体は存在しますからしっかり光量ロスは起こっていますけど。
(2025年11月5日) 中編につづく
■ポロプリズム双眼鏡のケラレの話(中編)
プリズム硝材の屈折率をどのぐらいにすれば(どの硝材を使えば)どの程度、視野にケラレが生じるのか?
スッキリさせたいので、双眼鏡のケラレのシミュレーションを行いました。
その前に、プリズムガラスによるケラレの原理について復習します。
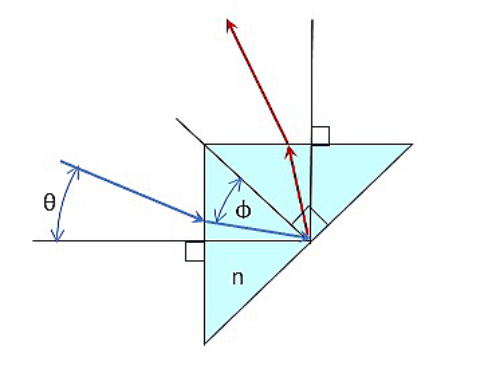
ポロプリズムは4個の直角プリズムが 90°ずつ回転方向を変えながら組み合わさったものと考えることができます。
図はその4個のうちの1個だけを示しています。
直角プリズムの45°反射面に光が斜めに入るとき、臨界角:φ(°)より大きい入射角で光が入ると全反射できず、面を透過してしまいます。
臨界角:φ(°)となる光線をさかのぼっていくと、プリズム入射面にある角度:θ(°)で入る光が臨界角を作っています。
つまり、プリズムが全反射するためには入射面にある限界角(θ)未満で光を入射させる必要があるということになります。
ガラスの屈折率をnとすると臨界角:φ(°)は
φ=sin-1(1/n)
またφとθの関係は
θ=sin-1{n*(45°-φ)}
となります。
吉田正太郎著 「望遠鏡光学・屈折編」p.58 表2.1 に同様の計算結果(硝材、屈折率、臨界角、限界角)を示した表があります。
いくつかの硝材と、アッベ数と硝材価格を追加して、nとφとθの表を作りました。
| 硝材 | 屈折率 | アッベ数 | 硝材価格** | 臨界角φ° | 入射限界角θ° |
| H2O(水) | 1.33 | 55.5 | − | 48.6 | -4.8 |
| BK7 | 1.52 | 64.2 | 1 | 41.2 | 5.7 |
| BaK4 | 1.57 | 36.6 | 1.35 | 39.6 | 8.5 |
| F2 | 1.62 | 36.4 | 1.45 | 38.1 | 11.2 |
| SSKN5 | 1.66 | 55.6 | 1.65 | 37.1 | 13.2 |
| LaKN13 | 1.69 | 50.9 | 2 | 36.2 | 15.0 |
| LaK10 | 1.72 | 55.3 | 2.05 | 35.5 | 16.4 |
| BaSF11* | 1.79 | 25.4 | 2.25 | 34.1 | 19.8 |
| LaSFN30 | 1.80 | 36.3 | 2.75 | 33.7 | 20.7 |
| SF57 | 1.85 | 25.4 | 3.5 | 32.8 | 23.0 |
| SF59 | 1.95 | 28.4 | 3.75 | 30.8 | 28.6 |
| S-TIH6*** | 2.00 | 26.1 | 4.5 | 30.0 | 31.3 |
注記 * 3CCDカメラのRGB分解プリズムに使用される硝材
** 価格はBK7を1とした場合の参考値
*** 最も屈折率の高い光学ガラスのひとつ
水(氷)の入射限界角がマイナスということは 直角プリズム入射面に垂直に光線を入れても臨界反射しないということを意味します。
また硝材価格は参考で、硝材が変わると加工・研磨の条件も変わるため、ノウハウがなければ容易に硝材を変えることはできず、価格比はもっと拡大します。
(2025年11月8日) 後編につづく
■ポロプリズム双眼鏡のケラレの話(後編)
前編と中編とで説明したことをつなげたいと思います。
ポロプリズムの入射限界角:θ があることにより、下図のようにプリズムによる制限枠(赤い矩形の枠)がかかったような状態になります。
この制限枠の一辺の長さは 2θで、視野中心部を観察しているときは制限枠の矩形の中心とここを通る光束の中心は一致しています。
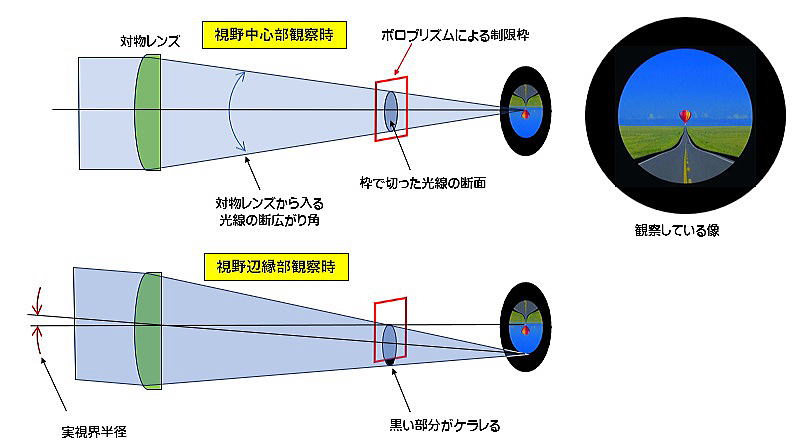
しかし視野の辺縁部を観察しているときには固定された視野枠(赤枠)に対し、光束の端の黒い部分が赤枠からはみ出し、プリズムを通れなくなります。
これにより光束の一部がケラレれて光量が低下します。 (観察像が欠けて見えるわけではありません。)
赤枠の大きさはポロプリズムの硝材の屈折率によってかなり変わります。
これをグラフにしてみました。
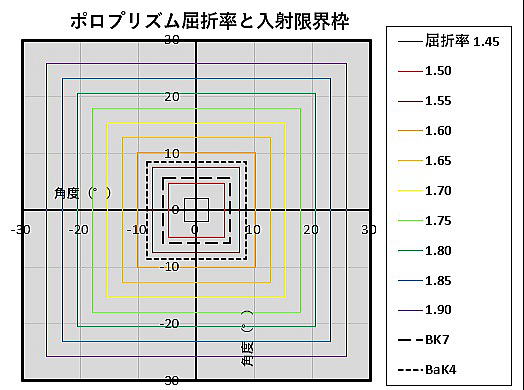
コストを度外視した場合に、屈折率が高い硝材ほど良いかというとそれは違います。
屈折率が高すぎるとこんどはプリズムの出射面で全反射を起こし光が出られなくなったり迷光が増えたりします。
何事もほどほどが良いようです。
また、枠を横切る光束の直径は双眼鏡の対物レンズのF値によって変わります。
そして視野の最周辺を観察しているときの光束のシフト量は双眼鏡の実視界によって変わります。
これらを計算するエクセルシートを作りました。 興味ある方は下のロゴをクリックしてダウンロードして使ってみてください。

白いセルに 上記の数値(屈折率、F値、実視界)を入れれば 赤枠と光束、そのシフトの様子をグラフに表示します。
(上述のプリズム以外の対物や接眼部分でのビネッティングの影響は計算に入っていません。)
グラフの横軸、縦軸の単位は角度の(°)です。
射出瞳径(単位mm)ではありませんが、グラフの円は射出瞳と相似形なので、ケラレのイメージはつかめると思います。
■ダハプリズム双眼鏡のケラレはどうなる?
ダハプリズム(シュミット・ペシャンプリズム)双眼鏡の場合のケラレはどうなるのでしょうか。
大雑把ですが下図のようになり、ケラレる方向は4辺(矩形)ではなく、一辺のみだったり、3辺だったりします。
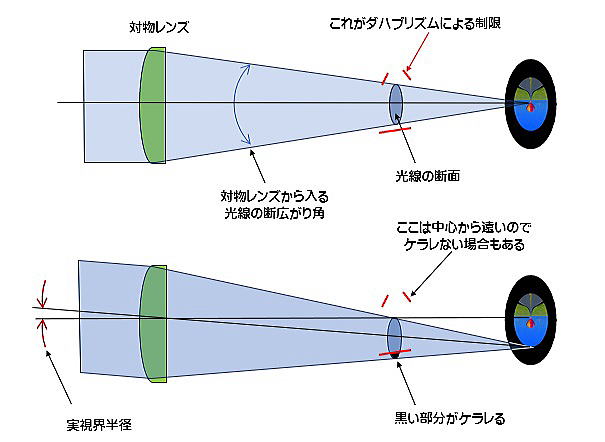
下側のケラレはポロプリズムと同じ 光軸入射角45°の反射面での臨界反射限界によるケラレです。
反射面の傾斜角は45°なので、ポロプリズムのケラレの一辺に相当します。
斜め上の小さなケラレ(2つ)はダハ面に入射する 光軸入射角49.2°の反射面の臨界反射限界によるケラレです。
後者のほうが角度的に遠い位置にあるためケラレは生じない場合もあります。
同じ硝材でプリズムを作った場合、ポロよりもダハのほうがケラレは目立たなくなりますね。
(2025年11月15日)
![]()

ホームへもどる